La relación matemática es el vínculo que existe entre los elementos de un subconjunto con respecto al producto de dos conjuntos. Una función implica la operación matemática para determinar el valor de una variable dependiente según el valor de una variable independiente. Toda función es una relación pero no toda relación es una función.
| Relación | Función | |
|---|---|---|
| Definición | Subconjunto de pares ordenados que corresponden al producto cartesiano de dos conjuntos. | Operación matemática que hay que realizar con la variable x para obtener la variable y. |
| Notación | x R y; x está relacionada con y. | y=ƒ(x); y es función de x. |
| Características |
|
|
| Ejemplos |
|
|
¿Qué es una relación matemática?
Se llama relación binaria de un conjunto A en un conjunto B o relación entre elementos de A y B a todo subconjunto C del producto cartesiano A x B.
Es decir, si el conjunto A está compuesto por los elementos 1, 2 y 3, y el conjunto B está compuesto por los elementos 4 y 5, el producto cartesiano de A x B serán los pares ordenados:
A x B= {(1,4), (2,4), (3, 4), (1,5), (2,5), (3,5)}.
El subconjunto C={(2,4), (3,5)} será una relación de A y B pues está compuesto por los pares ordenados (2,4) y (3, 5), resultado del producto cartesiano de A x B.
Concepto de relación
"Sean A y B dos conjuntos cualesquiera no vacíos, sea A x B el conjunto producto de ambos, es decir: A x B está formado por los pares ordenados (x, y) tales que x es el elemento de A y y lo es de B. Si en A x B se define un subconjunto cualquiera C, queda automáticamente determinada una relación binaria en A y B de la siguiente forma:
x R y si y solo si (x, y) ∈ C
(la notación x R y significa "x está relacionado con y").
Al conjunto A le llamaremos conjunto de partida y al conjunto B le llamaremos conjunto de llegada.
El dominio de la relación son los elementos que componen el conjunto de partida, mientras que el rango de la relación son los elementos del conjunto de llegada.
Ejemplo de relaciones matemáticas
El conjunto A de x elementos de hombres de una población y B es el conjunto de y elementos de mujeres de la misma población. Se establece una relación cuando "x está casado con y".
¿Qué es una función matemática?
Cuando hablamos de una función matemática de un conjunto A en un conjunto B nos referimos a una regla o mecanismo que relaciona los elementos del conjunto A con un elemento del conjunto B.
Concepto de función
"Sean x y y dos variables reales, se dice entonces que y es función de x si a cada valor que tome x le corresponde un valor de y."
La variable independiente es la x mientras que y es la variable dependiente o función:
y=ƒ(x)
El conjunto en que varía la x se denomina dominio de la función (original) y el de la variación de y rango de la función (imagen).
El conjunto de pares (x, y) tales que y=ƒ(x) se denomina grafo de la función; si se representan en unos ejes cartesianos se obtiene una familia de puntos que se denomina gráfica de la función.
Ejemplos de función
En matemáticas conseguimos muchos ejemplos de funciones. A continuación presentamos ejemplos de funciones emblemáticas.
Función constante
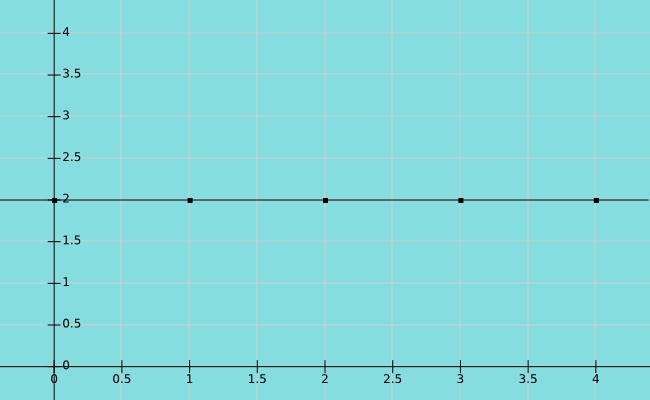
Una función se llama constante si el elemento del conjunto B que corresponde al conjunto A es el mismo. En este caso, a todos los valores de x corresponde el mismo valor de y. Así, el dominio son los números reales mientras el rango es un valor constante.
Función identidad
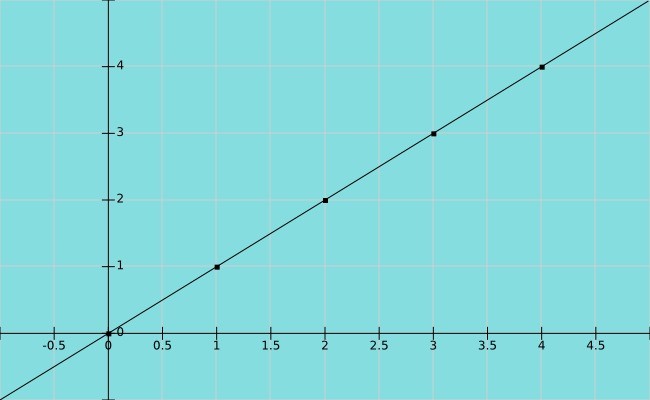
Supongamos que x es una variable y que y toma el mismo valor que x. Tenemos entonces una función identidad y=x, donde los pares (x, y) en la gráfica son (1,1), (2,2), (3,3) y así sucesivamente.
Función polinomial
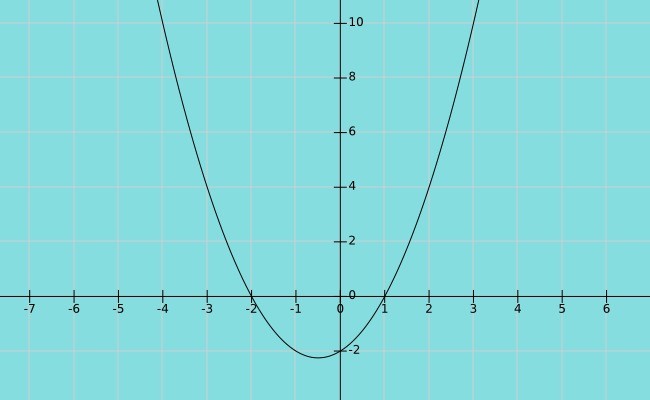
Una función polinomial cumple con la forma y= anxn+an-1+xn-1+....+a2x2+a1x+a0. La gráfica arriba muestra la función ƒ(x)=x2+x-2.
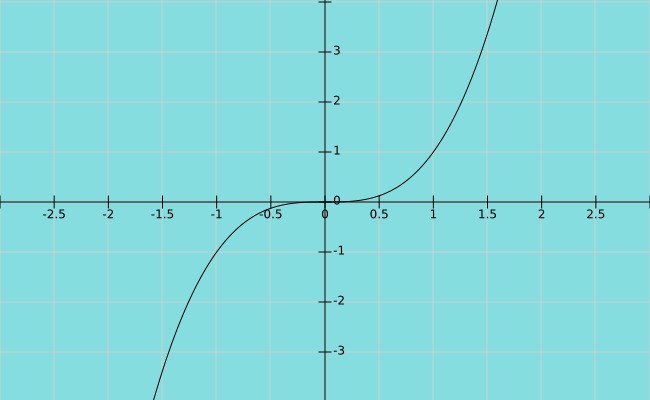
Supongamos ahora que la variable dependiente y es igual a la variable independiente x elevado al cubo. Tenemos la función y=x3, cuya gráfica se muestra abajo: